Taxonomy of Encoded Reasoning and LM Steganography
What exactly should we search for when investigating encoded reasoning or hidden messages? This post categorizes encoded reasoning and LM steganography.
In Hidden Reasoning in LLMs: A Taxonomy, the authors divide the area from the point of view of a monitor, following the recent shift away from the “faithfulness” of chains of thought toward monitorability (see Chain of Thought Monitorability). This taxonomy essentially proposes a naming scheme based on how dangerously reasoning tokens are externalized: from fully invisible (neuralese), to partially visible, to fully visible but encoded—overtly or covertly—and finally to unencoded and fully visible reasoning that merely fools a monitor (post-hoc justifications, etc.). You can imagine this division through the classic prisoners problem, where Alice and Bob devise an escape plan while Eve reads their messages. In this scenario, Alice and Bob can exchange their plan directly so Eve has no chance to read it, send messages that Eve can read, or fool Eve in some way.
However, this taxonomy omits important distinctions in encoded reasoning and sometimes conflates different forms of steganography. Specifically, it misses the class of steganography that operates not on a per-token basis but over larger texts (which differs from lexical or semantic steganography as per the taxonomy). Current watermarking / steganography algorithms (e.g. Scalable watermarking for identifying large language model outputs ) suggest that realistic steganographic capacity is low—i.e., a steganography algorithm might need many tokens (hundreds) to encode a single bit. The taxonomy also provides no separation between reasoning and messages. It focuses only on the attack vector (the safety monitor), but there are also defense properties to consider: stego security, stego capacity, and stego robustness.
Below is another taxonomy that targets encoded reasoning (or messages)—not neuralese phenomena or the attempts to fool a monitor. Encoded reasoning is, I believe, more likely to be developed by models because, as Chain of Thought Monitorability argues, we should neither develop continuous chains of thought (see Training Large Language Models to Reason in a Continuous Latent Space) nor train directly against monitors (see Monitoring Reasoning Models for Misbehavior and the Risks of Promoting Obfuscation).
Axis 1: Place of Encoded Tokens (I or E)
It is important to distinguish auto-generated tokens from prompted tokens, because prompted tokens may be re-tokenized differently during generation. This can mean that the actual tokens in a prompt differ from their original tokenization (see image below and here).
More specifically, consider tokens $(x_1, \dots, x_k, \dots, x_m)$, where $1…k$ are prompted (possibly re-tokenized) to an LLM and $k+1…m$ are auto-generated by it. The encoding is divided into:
- External (E): tokens at positions $1…k$ (possibly re-tokenized)
- Internal (I): tokens at positions $k+1…m$
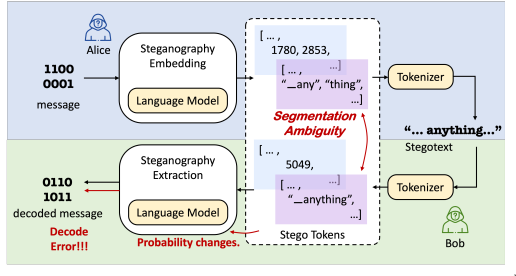
Figure 1 from Provably Secure Disambiguating Neural Linguistic Steganography
Axis 2: Function of Encoded Content (R or M)
The key distinction here is where encoding or decoding occurs.
- In encoded messages (M), one autoregressive token generation can perform either encoding or decoding of the same information.
- In encoded reasoning (R), both the encoding and decoding of the same information occur within a single model call.
Axis 3: Detectability Compared to Genuine Text
We compare the hidden content’s detectability against some unencoded, genuine text (covertext), drawn either from the monitor model or from human perception.
- Cryptographic (C): high (KL) divergence; the text is clearly ciphertext.
- Steganographic (S): low KL divergence, where the text attempts to conceal a secret. Steganography can be further divided by:
- Capacity: encoded bits per token or per kilobyte. High-density (HD) uses ≤10 tokens (10 is my guess) per bit; low-density (LD) uses ≥11 tokens per bit (watermarking-like).
- Security: higher vs. lower KL divergence, but non-cryptographic.
- Robustness: resistance to paraphrasing, re-tokenization, and similar modifications.
It is debatable whether one bit of hidden information qualifies as encoded reasoning (message) at all. For example, in the candidate-screening scenario discussed in Hidden in Plain Text, one bit of information might be transmitted simply through contextual hints—like Alice appearing sad to convey “sunny weather” and happy to convey “not sunny weather”—without any explicit encoding.
Axis 4: Encoding or Decoding Procedure Requirements
Deep Steganography (DS). As noted in How dangerous is encoded reasoning, steganography algorithms can be divided by whether the covertext distribution is available. This relates to “internal token layering” from Hidden Reasoning in LLMs: A Taxonomy. Specifically, encoding or decoding a token at position $j$ requires the distribution for the non-encoding token at $j$, given tokens $(i…j-1)$, where $i$ marks the start of the encoded content.
Axis 5: Cause or Elicitation of Encoding
- Prompted (P): Algorithm described in context
- Fine-tuned (F): Algorithm learned in the model’s weights
- Hybrid (H): Algorithm partially in context and partially in weights
Axis 6: External Tool Requirements
Determine whether external tools (T) are required—e.g., PRNGs, arithmetic coders, or self-sampling capabilities.
Final Taxonomy Summary
- Internal (I) or External (E)
- Reasoning (R) or Messages (M)
- Cryptography (C) or Steganography (S)
- Properties: capacity, security, robustness
- Requirements: self-sampling (deep steganography), external tools (ET)
- Elicitation: Prompted (P), Fine-tuned (F), Hybrid (H)